Voici quelques éléments pour répondre à cette question, de plus en plus existentielle pour les marins avec l’arrivée des hydrofoils.
Avant de répondre, prenons la question à l'envers.
Pourquoi les bateaux seraient limités en vitesse par la vitesse du vent ?
A priori, il n’y a pas de relation immédiate puisque le vent ne pousse pas le bateau mais crée une force qui entraîne le bateau.
Du point de vue de la physique, tant que la force qui entraîne (c’est à dire celle du vent) est strictement supérieure à celle qui freine alors le bateau accélère, c’est à dire que sa vitesse augmente (définition de l’accélération).
Ainsi donc, la vitesse du vent ne crée pas la “vitesse du bateau” mais une force propulsive. Il n’y a donc pas de lien immédiat entre la vitesse du vent et la vitesse du bateau.
Oublions les forces de traînée
Les forces de traînée sont tellement difficiles à modéliser que nous allons les oublier.
En effet, elles dépendent des formes du bateau, du poids, des vagues, de la texture du revêtement de la coque, de la texture des voiles. Donc de tellement d'éléments que la modélisation est impossible … en tous cas pour moi.
Cependant, quand nous utilisons des voiles, le vent vu par le bateau est le vent apparent, c’est à dire le vent réel (celui qui nous décoiffe sur la plage) et le vent vitesse, celui généré par la vitesse du bateau. Un petit schéma.

Le vent réel en rouge. La vitesse du bateau en vert (trait fin) et donc le vent vitesse qui est un vecteur opposé de la vitesse. En combinant vectoriellement (c’est à dire en deux dimensions dans notre cas) les deux vecteurs nous avons le vent apparent en bleu.

Nous voyons aisément que l’angle entre l’axe du bateau et le vent apparent diminue. Or, nous savons que cet angle ne peut pas diminuer jusqu’à zéro. Avec des voiles, il y a une limite de remontée au vent que nous allons appeler ALPHA (c’est toujours plus chic de prendre des lettres grecques pour des angles !).
Donc, pour un vent réel donné, la vitesse du bateau ne pourra pas dépasser une valeur correspondant au fait que le vent apparent ne peut pas venir d’un angle inférieur à ALPHA.
Maintenant, il va falloir calculer la vitesse en fonction de ALPHA (angle avec le vent apparent) et BETA (angle avec le vent réel).

Maintenant, que nous avons posé le problème, ressortons de nos grimoires quelques formules de trigonométrie (et oui, il fallait écouter en cours !).

Pour aller pas à pas dans le raisonnement nous allons calculer les dimensions sur les axes concernant “Vr”.

Ne revenons pas sur ces formules car c’est la définition même de la notion de cosinus (cos) et sinus (sin).
Occupons nous maintenant de l’angle ALPHA.

Encore une définition, celle de la tangente : - tg (ALPHA) = AA / BB, c’est à dire le côté opposé de l’angle divisé par le côté adjacent (il y un signe moins car le vecteur est dans le sens non habituel).
Or nous venons de voir que “AA” est égale à -Vr*sin(BETA), nous en déduisons facilement que “BB” = Vr*sin(BETA)/tg(ALPHA).
Et nous avons aussi vu que “CC” = -Vr*cos(BETA).
Et comme nous voyons sur le schéma que Vmax = BB + CC, nous avons notre formule.
Vmax = -Vr*cos(BETA) + Vr*sin(BETA)/tg(ALPHA) ce qui donne en simplifiant :
La limitation de l’angle du vent apparent
Rappel sur le vent apparent
Cependant, quand nous utilisons des voiles, le vent vu par le bateau est le vent apparent, c’est à dire le vent réel (celui qui nous décoiffe sur la plage) et le vent vitesse, celui généré par la vitesse du bateau. Un petit schéma.
Et la vitesse augmente …
Regardons ce que devient notre schéma lorsque la vitesse du bateau augmente.Nous voyons aisément que l’angle entre l’axe du bateau et le vent apparent diminue. Or, nous savons que cet angle ne peut pas diminuer jusqu’à zéro. Avec des voiles, il y a une limite de remontée au vent que nous allons appeler ALPHA (c’est toujours plus chic de prendre des lettres grecques pour des angles !).
Vitesse maximale théorique
Donc, pour un vent réel donné, la vitesse du bateau ne pourra pas dépasser une valeur correspondant au fait que le vent apparent ne peut pas venir d’un angle inférieur à ALPHA.
Maintenant, il va falloir calculer la vitesse en fonction de ALPHA (angle avec le vent apparent) et BETA (angle avec le vent réel).
Maintenant, que nous avons posé le problème, ressortons de nos grimoires quelques formules de trigonométrie (et oui, il fallait écouter en cours !).
Pour aller pas à pas dans le raisonnement nous allons calculer les dimensions sur les axes concernant “Vr”.
Ne revenons pas sur ces formules car c’est la définition même de la notion de cosinus (cos) et sinus (sin).
Occupons nous maintenant de l’angle ALPHA.
Encore une définition, celle de la tangente : - tg (ALPHA) = AA / BB, c’est à dire le côté opposé de l’angle divisé par le côté adjacent (il y un signe moins car le vecteur est dans le sens non habituel).
Or nous venons de voir que “AA” est égale à -Vr*sin(BETA), nous en déduisons facilement que “BB” = Vr*sin(BETA)/tg(ALPHA).
Et nous avons aussi vu que “CC” = -Vr*cos(BETA).
Et comme nous voyons sur le schéma que Vmax = BB + CC, nous avons notre formule.
Vmax = -Vr*cos(BETA) + Vr*sin(BETA)/tg(ALPHA) ce qui donne en simplifiant :
Vmax = Vr * (-cos (BETA)+ sin(BETA)/tg ALPHA)
Et la vitesse du vent Apparent ?
Au point où nous en sommes, calculons la vitesse du vent apparent et nous aurons fini nos formules.Notre vent apparent c’est la grosse flèche bleue. Pythagore va nous aider avec sa formule (⋀2 signifie au carré, notation empruntée à l’informatique et beaucoup plus pratique que celle des mathématiques) :
(VentAppMax)⋀2 = (Vr*sin(BETA)/tg(ALPHA) ) ⋀2 + Vr*sin(BETA) ⋀2 et par simplification :
VentAppMax = Vr * sin(BETA) * SQRT (1+ 1/tg(ALPHA) ⋀2 )
Ouf, la partie théorique est maintenant finie. Passons aux cas pratiques.
Quelques simulations avec les formules
Vitesse du bateau et du vent apparent
Un premier tableau reprend la vitesse du bateau et celle du vent apparent pour un angle ALPHA fixe.
Peut-on aller à 2 fois, 3 fois la vitesse du vent ?
Passons maintenant à la VMG
Vous vous rappelez la VMG ? velocity made good, c’est à dire la capacité d’un bateau à aller à un point au vent (0° du vent réel) ou un point sous le vent (180° du vent réel) en schématisant un peu.
La VMG est donc simplement la projection de la vitesse du bateau sur l’axe de vent réel, ce qui correspond à la vitesse du bateau (vecteur vert) multiplié par le cosinus de l’angle (180-BETA).
Rappelons que cos(180-BETA) = - cos(BETA)
VMGmax = -Vr * cos (BETA) * (-cos (BETA)+ sin(BETA)/tg ALPHA)
Donc, pour remonter au vent, il faut être à 60° du vent réel et pour aller sous le vent à 150° du vent réel.
Hélas, ceci n’est valable que si vous êtes au près serré du point de vue du vent apparent.
Le calcul optimal des angles
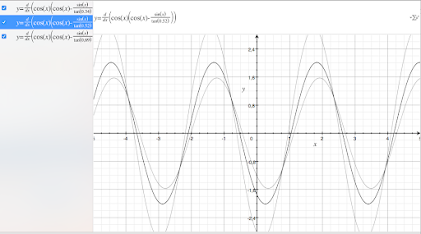
Réalisons trois courbes avec cette VMG pour des angles ALPHA de 20° (0,34 radian), 30° (0,52 radian) et 40° (0,69 radian).
Maintenant nous pouvons réaliser la dérivée de ces fonctions pour connaitre les angles idéaux c'est à dire un peu moins approximatif que le tableau Excel précédent.
Le grapher d'Apple fait les calculs pour nous.
- 1 radian donne 57 ° environ
- 2,6 radian donne 150° environ, ce qui corrobore bien les précédents calculs.
Pour ceux qui ont choisis Spécialité Maths,
d(VMGmax)/dBeta = -Vr * (cos (BETA) * (sin (BETA)+ cos(BETA)/tg ALPHA)
+Vr * (-sin(BETA) * (-cos (BETA)+ sin(BETA)/tg ALPHA)
= -Vr *[2*cos (BETA) * (sin (BETA) + (sin(BETA)^2 - cos(BETA)^2)/Tg(ALPHA)]
A ce stade, il faut trouver les racines : finalement c'est bien un grapher :-)
Confrontation avec le réel
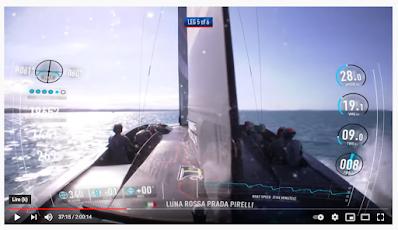
Le rapport vitesse du bateau / vitesse du vent est de 42,4/11,6= 3,65 est vraiment excellent (peut être pour cela qu'ils ont gagné ;-)
Il est difficile de conclure car ce sont des vitesses instantanées tant pour le vent que pour le bateau mais cela donne une première idée.
La voile est bien moins bordée : on voit bien l'arrière sur la droite de l'image. L'angle est de 2338-015= 63° qui nouos rapproche des 57° du grapher pour un angle théorique de 20° de remontée au vent.
Une dernière image pour vos propres analyses.
Conclusion
Mais alors, faut-il aussi que les amoureux de glisse apprennent à faire du près serré et ne plus laisser ce talent uniquement aux besogneux de croisière ;-)
PS: une bonne âme pour vérifier les calculs ?