Une dérive  torique

J'ai toujours été surpris du manque d'évolution dans les dérives des dériveurs : le concept n'a pas bougé depuis ... longtemps alors que c'est un élément essentiel de nos coques.

Le profil d'une dérive actuel ressemble à une planche ; lorsque le bateau gîte elle ne sert quasiment à rien saut à resaler le bateau une fois à 90°.

Voici un axe de réflexion.

Voici un rouge notre coque de bateau. Uniquement le fond est représenté mais je connais votre imagination et il vous suffit d'ajouter quelques planches rouges pour avoir un magnifiques Vaurien, ou une Caravelle  ou un galion.

En vert, le (enfin les) puit de dérive.

En jaune, la dérive.

Voyons un peu notre dérive à l'action. Elle est toujours tenu par les deux parties du puits de dérive. Les puits et la dérive étant sur une forme torique (circulaire en 3D), cela peut coulisser.

Cerise sur le gâteau, le profil de la dérive est adapté l'amure.

On peut désormais avoir un profil adapté sur chaque coté et abandonner notre profil symétrique moins efficace.

Maintenant un peu de BloskScad pour arriver à tout cela. Dans un premier temps, voyons notre profil de dérive.

Le profil

Une fonction de Béziers avec les bons paramètres. A ce stade, pas de calcul hydrodynamique de la forme, ce sera pour une autre fois car elle dépend du bateau, de sa vitesse de son poids.

Pour la fonction de Béziers, un autre Post est disponible.

La dérive

Une fois que le profil est fait, la programmation est assez simple.

Une extrusion circulaire sur le profil et une soustraction pour n'avoir qu'un demi-cercle.

Notez cependant, cela m'a pris un peu de temps de réglage, le bloc "translation" entouré de jaune sur l'image associé à la rotation circonscrite. Elle permet d'avoir ce tore avec le profile initial.

Le puits de dérive

Le puits de dérive part aussi du profil creux et y ajoute une échelle.

Nous voyons sur le schéma le principe. En fait le puits est une dérive à une échelle un peu supérieur et avec des cube en soustraction pour supprimer les parties non désirées.

Le cube violet a été sorti du programme pour illustrer le principe.

et voici nos deux puits définitis.

Et voila le puits et sa dérive

Le (bout) de coque

deux plaques un peu inclinées et en soustraction le profil. La difficulté est que le profil est creux donc il reste de la matière au milieu. Je n'ai pas encore trouvé comment remplir un profil, surtout s'il n'est pas convexe. 

En effet, la fonction HULL qui permet de remplir rend les surface convexes ... ce qui nous arrange pas pour notre profil. 

En conclusion

l'histoire de la dérive n'est pas finie car on doit pouvoir faire encore quelques améliorations à ce premier jet. J'ai quand même une pensée émue pour le charpentier de marine qui devrait réaliser un tel système sans imprimante 3D ;-)

 

BlockScad : polynômes de Lagrange

Nous avons déjà présenté deux familles de courbes : celle de Bézier et celles de GrandPierre. Ces courbes sont pratiques et donnent de nombreuses possibilités, cependant il est compliqué de trouver les bons paramètres lorsque l'on veut passer par des points connus.

Dans cet article nous allons préparer une courbe mathématiquement simple, c'est à dire polynomiale, qui passe par trois points connus, en utilisant les polynômes de Lagrange.(voir  https://fr.wikipedia.org/wiki/Interpolation_lagrangienne )

Dans Blockscad nos trois points seront représentés par six paramètres : (Ax,Az) ; (Bx,Bz) ; (Cx,Cz)

Tout d'abord, il nous faut écrire chacun des trois polynômes qui s'annulent pour deux des trois points.

La(i) = (i-Bx)(i-Cx) / (Ax-Bx)(Ax-Cx) On peut remarquer que pour i valant Bx ou Cx ce polynôme sera nul et pour x valant Ax, ce polynôme vaut 1.

Lb(i) = (i-Ax)(i-Cx) / (Bx-Ax)(Bx-Cx). idem ce polynôme est nul pour Ax et Cx

Lc(i) = (i-Ax)(i-Bx)/(Cx-Ax)(Cx-Bx). De la même façon ce polynôme est nul pour Ax et Bx.

Voyons cela sous BlockScad.

Maintenant, il convient d'additionner ces trois polynômes avec les bons coefficients. Comment sont calculés ces coefficients ?
Pour i=Ax, Lb et Lc sont nul et La vaut 1. Il suffit donc pour passer par Az de multiplier par Az. Et de même pour les autres.

Pour passer par quatre points, c'est un peu plus long mais c'est le même principe.

Reprenons, notre système de boucle et de translation pour faire la courbe correspondante. Ne pas oublier que la boucle commence à Ax et fini (par convention) à Cx. Il faudra donc veiller à ce que les trois points soit toujours dans l'ordre croissant des abcisses.

Il ne nous reste plus qu'à faire un petit essai pour voir si cela marche (et tout recommencer sinon, mais cela vous le voyez pas ;-)

En premier temps, dessinons trois points.

Et appliquons les coordonnées de ces trois points à notre polynôme de Lagrange.

Rapidement, passons à une courbe avec 4 points.

Nous avons créé les variables Dx et Dz et nous avons complété les formules de façon assez mécanique. Ne pas oublier de changer la boucle pour qu'elle finisse à Dx.

Nous rajoutons le point vert dans le dessin. Attentions, il faut décaler les points qui ne sont pas dans l'ordre.

Et pour terminer, mais sans explication car le principe est connu, la version à 5 points.

Et pour terminer cet article, voici la courbe qui passe par les précédents points et le point rouge.

Plus le nombre de points augmentent plus la courbe est censée être lissée.

Engrenage et développante du cercle

La développante du cercle

Aujourd'hui nous allons explorer le monde des engrenages.

Dans Wikipédia, nous apprenons que la développante du cercle est une courbe mathématique ayant des propriétés géométriques qui font qu'elle est utilisée pour dessiner les engrenages. https://fr.wikipedia.org/wiki/D%C3%A9veloppante_du_cercle

Commençons donc par construire un cercle en deux dimensions. Cependant pour vous rappeler la construction de fonction nous allons utiliser les courbes paramétriques du cercle :

• x=R.cos(t)
• y=R.sin(t)

pour t variant de 0° à 360°

Maintenant, utilisons la formule donnée par Wikipédia pour la développante :

• x = R.(cos(t)+t.sin(t))
• y = R.(sint(t)-t.cos(t))

Voilà ce que cela donne.

Pas terrible ! en regardant le dessin on voit quelque point qui partent vers la gauche mais cela ne ressemble pas au dessin de Wikipedia.

Je montre cela car il y un truc : la courbe donnée par Wikipédia et sur tous les sites est une courbe ou (t) est en radian. Par contre blockScad utilise les degrés pour ses fonctions trigonométriques (la famille à laquelle sin et cos appartiennent).

il faut donc changer (t) en radian pour l'exprimer en degré avec une simple règle de trois car PI radian = 180 degré.

et voici le résultat, beaucoup plus compatible la référence du savoir mondial. 

Attention aux unités, elle sont souvent implicites, donc restons vigilant.

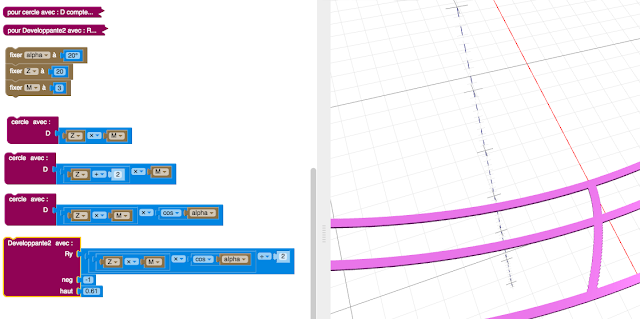
Quelques modifications sur le bloc de la développante pour rajouter deux paramètres, outre le diamètre du cercle de référence déjà présent :

1. "neg" pour faire partir la courbe dans l'autre sens, c'est à dire un "-1" pour la variable "y"
2. "haut" pour facilement faire varier la longueur de cette courbe spirale

Une roue dentée

Maintenant, passons aux engrenages sur la base d'un tutoriel utilisant un logiciel de dessin.

https://www.genapart.com/2016/01/05/dessinez-vos-engrenages/ 

De notre coté, nous allons suivre ce tutoriel mais en utilisant que des formules mathématiques, dans la mesure du possible.

L'image ci-dessous, issu du tutoriel précédent,  reprend les différentes paramètres et les définitions.

Nous allons construire un engrenage de 20 dents (Z=20) et de module 3 mm (M=3) :

1. un premier cercle de diamètre primitif (Dp = M.Z)
2. un deuxième cercle de diamètre extérieur (De = (Z+2).M
3. le cercle de base (Db = Dp.cos(alpha)). alpha est l'angle de la ligne d'action.

Pour l'instant, pas de souci particulier grâce à notre petite fonction "cercle" dont nous avons changé la variable d'entrée pour passer en diamètre.

Par contre, nous allons gagner du temps dans les phases suivantes car  en lieu et place d'une construction géométrique par succession d'arc de cercle nous allons utiliser notre formule magique de Wikipédia.

il faut régler manuellement le paramètre "haut". C'est fait en deux ou trois essais.

Hélas, nous ne pouvons pas compter sur des essais. il faut donc trouver ce paramètre par calcul. Le point d'intersection entre la développante et le cercle extérieur répond à deux équations : celle de la développante et celle du cercle.

Dans le dessin suivant, le récapitulatif.

Donc nous cherchons la valeur de (t) qui crée le point (A,B) avec pour la développante :

A = (ZMcos(alpha)/2).(cos(t)+t.sin(t))

B = (ZMcos(alpha)/2).(sint(t)-t.cos(t))

d'autre part, on sait que (A,B ) est sur le cercle extérieur donc A^2 + B^2 = ((Z+2)M/2)^2 (théorème de Pythagore)

on simplifie par /2 et M et on obtient :

1. Z^2[cos(t)+t.sin(t)]^2 + [sin(t)-t.cos(t)]^2 = (Z+2)^2/cos2(alpha)
2. cos2(t)+2tcos(t)sin(t))+t^2sin2(t) + sin2(t) - 2tsin(t)cos(t)+t^2cos2(t) = (Z+2)^2/(Z^2.cos2(alpha)) en développant
3. 1+0+t^2.(1) = (Z+2)^2/Z^2cos2(alpha) par regroupement et application de cos2+sin2 = 1
4. t= racine carrée ((Z+2)^2/Z^2cos2(alpha) - 1)

et voilà le travail. Faut reconnaitre que cela plus chic, une bonne formule !

Maintenant, nous traçons le cercle de pied dont le diamètre est Di = Dp -2,5.M soit Z-2.5M comme nous le demande le tutoriel.

En suivant le tutoriel, il faut tracer un trait entre le cercle de pied et la développante.

Ceci se fait avec une boucle qui va entre le rayon du cercle de pied et le rayon du cercle de base.

Ensuite, le tutoriel demande de voir l'angle entre la droite initiale de départ de la développante (en orange sur le dessin du dessous) et la droite qui intersecte la développante au niveau du cercle primitif (le trait en pointillé sur le dessin). En effet, c'est à cet endroit précis que la dent touche la dent de l'autre pignon.

Comme nous n'avons pas de possibilité de voir sur le logiciel, il nous faut à nouveau faire un calcul.

Dans un premier temps, trouvons la variable (t). Même principe que précédemment mais ce n'est pas le même cercle.

Donc nous cherchons la valeur de (p) qui crée le point (C,D) avec pour la développante :

C = (ZMcos(alpha)/2).(cos(p)+p.sin(p))

D = (ZMcos(alpha)/2).(sint(p)-p.cos(p))

d'autre part, on sait que (C,D) est sur le cercle primitif donc C^2 + D^2 = (ZM/2)^2 (théorème de Pythagore)

on simplifie par /2, Z et M et on obtient :

1. [cos(p)+t.sin(p)]^2 + [sin(t)-t.cos(p)]^2 = 1/cos2(alpha)
2. cos2(p)+2p.cos(p)sin(p))+t^2sin2(p) + sin2(p) - 2p.sin(p)cos(p)+t^2cos2(p) = 1/(cos2(alpha) en développant
3. 1+0+t^2.(1) = 1/cos2(alpha) par regroupement et application de cos2+sin2 = 1
4. t= racine carrée (1/cos2(alpha) - 1) = tangente(alpha) après petits calculs pas bien compliqués (trop horrible, diraient mes filles !)

Ce serait trop simple si c'était fini. Il faut trouver l'angle de ces deux droites. Hors nous savons que la tangente de cet angle est D/C, et donc l'angle est ATAN (D/C), ATAN étant la fonction ArcTangente que Blockscad a la bonne idée de mettre à disposition.

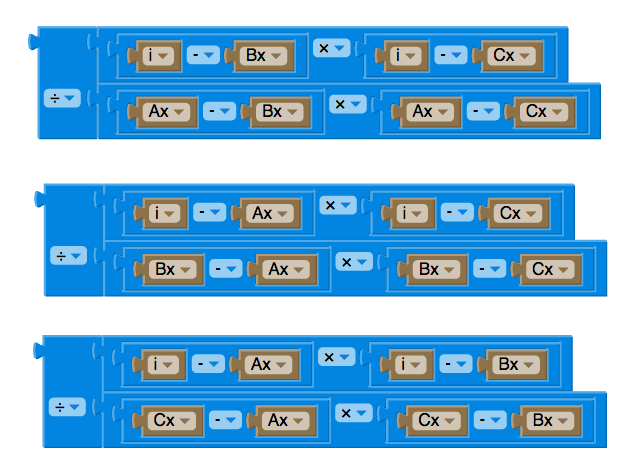
En simplifiant D/C et en appliquant notre résultat pour (p), nous obtenons :

Ce qui est assez proche du 0.90° trouvé dans le tutoriel. Regardez le code, il ne faut pas oublier de rajouter notre conversion d'angle dans les fonctions SIN et COS.

Pour contrôler, nous avons utilisé la fonction text 2D pour afficher le résultat. 

Ce n'est pas fini ! Il faut tracer la droite qui représente l'axe de la dent (360/4Z)+notre précédent décalage.

Continuons en traçant la droite avec le décalage d'ans l'autre sens.

Avant d'aller plus loin, nous allons fabriquer une évolution de notre block "cercle" pour faire des arcs de cercle. J'ai le plaisir de vous présenter "cercle2" :

 Ce n'est pas non plus, l'invention du siècle, mais cela va être bien pratique.

Le tutoriel nous demande de supprimer le cercle de pied et de ne garder que la distance entre le bas de la dent et la droite à décalage négatif.

Nous allons utiliser simplement notre nouveau module de cercle, le démarrer à zéro et le terminer à l'angle de rotation de la droite.

et bien sûr, l'ancien module qui traçait le pied de cercle est désactivé. Continuons pour le cercle extérieur.

Le diamètre sera celui du cercle extérieur (nous l'avons déjà), l'angle de départ est l'angle de rotation que nous avons tracé (il faudra peut être voir  à changer le signe). Concentrons nous donc sur l'ange d'arrivé, qui correspond à l'intersection entre la développante et le cercle extérieur.

Nous avons déjà calculé ce point : (A,B). Donc l'angle se calcule par l'arcTangente avec des commentaires sous le dessin.

Le calcul avait déjà été fait et se matérialise par le paramètre "haut" de la développante. Se paramètre a été nommé variable "EE" pour plus de lisibilité.

Ensuite on retrouve se paramètre dans notre formule avec ATAN (sint(t)-tcos(t))/(cost(t)-tsin(t)).

A ce stade, le tutoriel n'utilise que les fonctions de miroir et de boucle pour réaliser les Z dents.

Ramenons la dent sur l'axe des X et supprimons les cercles initiaux. Il suffit d'utiliser la fonction rotation suivant Z de la droite tracée.

un petit coup de miroir et une boucle plus loin.

et nous avons notre engrenage pour Z=20.

et pour Z=11

Effectivement, cela vaut le coup de faire les calculs au moins une fois. ces blocs sont en partage libre de droit sur le site de Blockscad.

 

Je ne résiste pas au plaisir d'un dernier dessin avec une extrusion.

En conclusion, il faudrait une bonne âme pour vérifier les calculs ;-) 

Boulier Elliptique compatible Blockchain

Ce nouveau post va nous permettre de réaliser une boulier elliptique. Nous verrons en conclusion du post tous les intérêts dans le domaine des blockchain qui font un usage immodéré de la cryptographie elliptique.

Revenons un peu sur les courbes elliptiques. Comme l'explique Wikipédia ce sont des courbes de la forme Y^2=aX^3+bX+c  soit Y = RacineCarré  (aX^3+bX+c) pour une demi-courbe.

ce qui en BlockScad se traduit par le bloc suivant (pour les nouveaux sur ce site, voir les étapes précédentes sur BlockScad) avec des paramètres soigneusement choisi. Nous reviendrons sur le choix en fin de post.

Avec ce block nous allons construire une première courbe.

la fonction Kx est une boucle entre -2.34862 (la valeur de X pour que Y soit nul et 4 pour ne pas faire un boulier trop grand.

Sur le graphique, l'axe rouge est le X et l'axe vert est le Y.

A ce stade, réalisons la courbe complète en utilisant une symétrie par rapport au plan XZ

Ne vous inquiétez pas, la taille des branches est la même : c'est simplement l'affichage 3D qui donne une impression de dissymétrie.

Maintenant, nous voulons ajouter un objet qui puisse facilement glisser sur la courbe elliptique pour agir comme tangente à la courbe.

Nous allons décrire dans le détail les différentes étapes.

En premier temps, un anneau torique (en bleu) qui devra coulisser sur la courbe. Le programme ne pose aucun souci. Je vous passe les détails sur le choix des mesures : un peu de calcul très simple et surtout beaucoup d'essais et de vérification sous plusieurs angles du dessin 3D.

En jaune, un cylindre creusé avec seulement 5 faces et en rouge l'axe qui rentre dans le cylindre.

Maintenant il s'agit de :

1. positionner le tore sur la courbe
2. d'orienter le tore pour qu'il soit bien perpendiculaire à la courbe.

Pour positionner notre axe sur la courbe, nous allons utiliser la fonction qui nous donne la courbe. Regardez le programme ci-dessous.

Nous avons seulement ajouter une fonction TRANSLATION  avec X et Y qui est le résultat de la courbe elliptique. Le paramètre "bool" est simplement à 1 ou -1 suivant que l'on veut un place sur les Y positifs (demi-courbe du haut) ou sur les Y négatifs (demi-courbe du bas).

En complément, nous avons mis ce petit bout de code sous forme d'un module "tangente" pour facilement passer les paramètres.

Mais, comme nous pouvons le constater sur la représentation 3D, ce nouvel objet interfère avec la courbe. Il est donc temps de faire la deuxième partie du programme, celle qui va orienter l'axe rouge comme tangente à la courbe.

Au passage, remarquons que le tore bleu et le cylindre jaune seront donc à 90° de la tangente.

Entouré d'un liseré jaune, nous avons ajouté une rotation verticale, c'est à dire suivant l'axe des Z.

Pour ce faire nous utilisons les propriétés suivantes des mathématiques du secondaire (je sais la seconde c'est loin mais ce n'est pas pour rien que l'on devait apprendre ces leçons ;-) 

1. la tangente de l'angle à un courbe est donné par sa dérivée
2. l'angle est donc donné par la fonction inverse de la tangente, c'est-à-dire ArcTangente (ou ATAN en BlocScad)
3. et comme nous l'avons remarqué précédemment, il faut rajouter 90 pour rester orthogonal à la tangente
4. et toujours notre variable "bool" pour choisir si c'est en haut ou en bas sur la courbe

Donc la formule du haut reste simple à comprendre. Il nous reste à calculer la dérivée de la courbe elliptique.

C'est le module en dessous. Petit rappel nécessaire sur les dérivées de RacineCarré ? Je vous ai trouvé un site tout à fait adapté. https://homeomath2.imingo.net/derirac.htm

et voici donc notre belle courbe avec 2 droites tangentes.

le reste du projet est un peu de cosmétique pour pouvoir en faire une impression 3D.

On ajoute un cadre pour mieux tenir la courbe et aussi pour la prochaine étape.

Pas de souci particulier pour ce programme. Les bonnes valeurs par essais successifs (comme d'hab !)

Maintenant, rajoutons une réglette verticale.

Bien qu'un peu long, le module est très simple. Il s'agit d'une réglette qui peut coulisser sur le cadre (axe des X) et qui représente une vertical sur l'axe des Y.

A partir de maintenant, nous avons tous les éléments pour graduer notre règle. Si nous partons du principe que la tangente est au point (1) le point (2) est représenté sur la figure.

d'où l'intérêt de réaliser la réglette.

le trois se déduit de l'intersection entre le 1 et le 2. 

Concernant l'impression 3D, il faut faire cela en deux fois. la courbe et le cadre puis les axes. Même si en dessous vous avez une simulation de la règle complète.

Revenons, un peu sur la courbe elliptique. Voici ce que cela donne sous GEOGEBRA.

Pour bien vous convaincre que le choix des paramètres est très important, voici un nouveau dessin avec des paramètres un peu changés.

et c'est ainsi que nous découvrons que nous aurions pu tomber dans un poisson d'avril ... uniquement si les paramètres initiaux avaient été mal choisis ;-)

Et pour tous ceux qui ont eu la patience de lire jusqu'au bout, voici le bidule réalisé avec SCULPTEO.

Il y a surement quelques optimisations à faire d'autant plus que cela n'a vraiment rien d'un boulier ;-)