mercredi 14 octobre 2020
dimanche 11 octobre 2020
Une dérive torique
J'ai toujours été surpris du manque d'évolution dans les dérives des dériveurs : le concept n'a pas bougé depuis ... longtemps alors que c'est un élément essentiel de nos coques.
Le profil d'une dérive actuel ressemble à une planche ; lorsque le bateau gîte elle ne sert quasiment à rien saut à resaler le bateau une fois à 90°.
Voici un axe de réflexion.
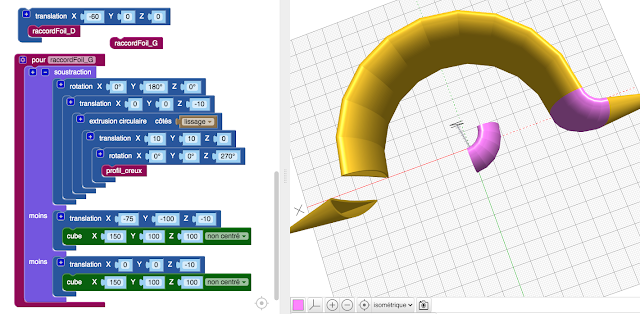
Voici un rouge notre coque de bateau. Uniquement le fond est représenté mais je connais votre imagination et il vous suffit d'ajouter quelques planches rouges pour avoir un magnifiques Vaurien, ou une Caravelle ou un galion.
En vert, le (enfin les) puit de dérive.
En jaune, la dérive.
Voyons un peu notre dérive à l'action. Elle est toujours tenu par les deux parties du puits de dérive. Les puits et la dérive étant sur une forme torique (circulaire en 3D), cela peut coulisser.
Cerise sur le gâteau, le profil de la dérive est adapté l'amure.
On peut désormais avoir un profil adapté sur chaque coté et abandonner notre profil symétrique moins efficace.
Maintenant un peu de BloskScad pour arriver à tout cela. Dans un premier temps, voyons notre profil de dérive.
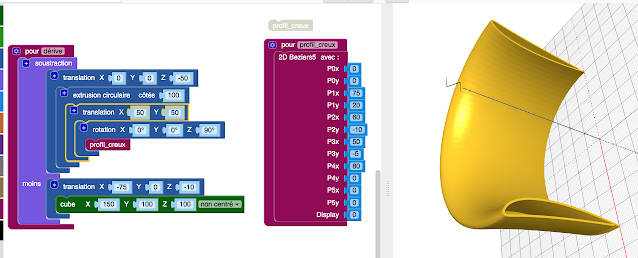
Le profil
Une fonction de Béziers avec les bons paramètres. A ce stade, pas de calcul hydrodynamique de la forme, ce sera pour une autre fois car elle dépend du bateau, de sa vitesse de son poids.
Pour la fonction de Béziers, un autre Post est disponible.
La dérive
Une fois que le profil est fait, la programmation est assez simple.
Une extrusion circulaire sur le profil et une soustraction pour n'avoir qu'un demi-cercle.
Notez cependant, cela m'a pris un peu de temps de réglage, le bloc "translation" entouré de jaune sur l'image associé à la rotation circonscrite. Elle permet d'avoir ce tore avec le profile initial.
Le puits de dérive
Le puits de dérive part aussi du profil creux et y ajoute une échelle.
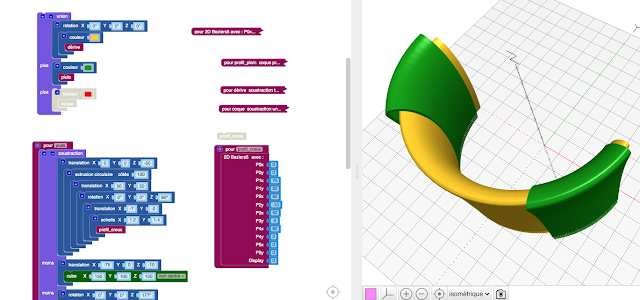
Nous voyons sur le schéma le principe. En fait le puits est une dérive à une échelle un peu supérieur et avec des cube en soustraction pour supprimer les parties non désirées.
Le cube violet a été sorti du programme pour illustrer le principe.
et voici nos deux puits définitis.
Et voila le puits et sa dérive
Le (bout) de coque
deux plaques un peu inclinées et en soustraction le profil. La difficulté est que le profil est creux donc il reste de la matière au milieu. Je n'ai pas encore trouvé comment remplir un profil, surtout s'il n'est pas convexe.
En effet, la fonction HULL qui permet de remplir rend les surface convexes ... ce qui nous arrange pas pour notre profil.
En conclusion
l'histoire de la dérive n'est pas finie car on doit pouvoir faire encore quelques améliorations à ce premier jet. J'ai quand même une pensée émue pour le charpentier de marine qui devrait réaliser un tel système sans imprimante 3D ;-)
samedi 2 mai 2020
BlockScad : polynômes de Lagrange
Dans cet article nous allons préparer une courbe mathématiquement simple, c'est à dire polynomiale, qui passe par trois points connus, en utilisant les polynômes de Lagrange.(voir https://fr.wikipedia.org/wiki/Interpolation_lagrangienne )
Dans Blockscad nos trois points seront représentés par six paramètres : (Ax,Az) ; (Bx,Bz) ; (Cx,Cz)
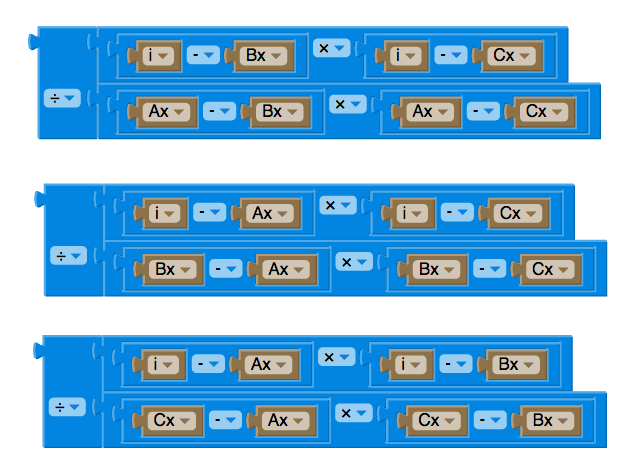
Tout d'abord, il nous faut écrire chacun des trois polynômes qui s'annulent pour deux des trois points.
La(i) = (i-Bx)(i-Cx) / (Ax-Bx)(Ax-Cx) On peut remarquer que pour i valant Bx ou Cx ce polynôme sera nul et pour x valant Ax, ce polynôme vaut 1.
Lb(i) = (i-Ax)(i-Cx) / (Bx-Ax)(Bx-Cx). idem ce polynôme est nul pour Ax et Cx
Lc(i) = (i-Ax)(i-Bx)/(Cx-Ax)(Cx-Bx). De la même façon ce polynôme est nul pour Ax et Bx.
Voyons cela sous BlockScad.
Maintenant, il convient d'additionner ces trois polynômes avec les bons coefficients. Comment sont calculés ces coefficients ?
Pour i=Ax, Lb et Lc sont nul et La vaut 1. Il suffit donc pour passer par Az de multiplier par Az. Et de même pour les autres.
Pour passer par quatre points, c'est un peu plus long mais c'est le même principe.
Reprenons, notre système de boucle et de translation pour faire la courbe correspondante. Ne pas oublier que la boucle commence à Ax et fini (par convention) à Cx. Il faudra donc veiller à ce que les trois points soit toujours dans l'ordre croissant des abcisses.
Il ne nous reste plus qu'à faire un petit essai pour voir si cela marche (et tout recommencer sinon, mais cela vous le voyez pas ;-)
En premier temps, dessinons trois points.
Rapidement, passons à une courbe avec 4 points.
Nous avons créé les variables Dx et Dz et nous avons complété les formules de façon assez mécanique. Ne pas oublier de changer la boucle pour qu'elle finisse à Dx.
Nous rajoutons le point vert dans le dessin. Attentions, il faut décaler les points qui ne sont pas dans l'ordre.
Et pour terminer, mais sans explication car le principe est connu, la version à 5 points.
Et pour terminer cet article, voici la courbe qui passe par les précédents points et le point rouge.
Plus le nombre de points augmentent plus la courbe est censée être lissée.
mardi 28 avril 2020
Un bateau peut-il aller plus vite que le vent ?
Voici quelques éléments pour répondre à cette question, de plus en plus existentielle pour les marins avec l’arrivée des hydrofoils.
Pourquoi les bateaux seraient limités en vitesse par la vitesse du vent ?
Oublions les forces de traînée
Les forces de traînée sont tellement difficiles à modéliser que nous allons les oublier.La limitation de l’angle du vent apparent
Rappel sur le vent apparent
Cependant, quand nous utilisons des voiles, le vent vu par le bateau est le vent apparent, c’est à dire le vent réel (celui qui nous décoiffe sur la plage) et le vent vitesse, celui généré par la vitesse du bateau. Un petit schéma.
Et la vitesse augmente …
Regardons ce que devient notre schéma lorsque la vitesse du bateau augmente.Nous voyons aisément que l’angle entre l’axe du bateau et le vent apparent diminue. Or, nous savons que cet angle ne peut pas diminuer jusqu’à zéro. Avec des voiles, il y a une limite de remontée au vent que nous allons appeler ALPHA (c’est toujours plus chic de prendre des lettres grecques pour des angles !).
Vitesse maximale théorique
Donc, pour un vent réel donné, la vitesse du bateau ne pourra pas dépasser une valeur correspondant au fait que le vent apparent ne peut pas venir d’un angle inférieur à ALPHA.
Maintenant, il va falloir calculer la vitesse en fonction de ALPHA (angle avec le vent apparent) et BETA (angle avec le vent réel).
Maintenant, que nous avons posé le problème, ressortons de nos grimoires quelques formules de trigonométrie (et oui, il fallait écouter en cours !).
Pour aller pas à pas dans le raisonnement nous allons calculer les dimensions sur les axes concernant “Vr”.
Ne revenons pas sur ces formules car c’est la définition même de la notion de cosinus (cos) et sinus (sin).
Occupons nous maintenant de l’angle ALPHA.
Encore une définition, celle de la tangente : - tg (ALPHA) = AA / BB, c’est à dire le côté opposé de l’angle divisé par le côté adjacent (il y un signe moins car le vecteur est dans le sens non habituel).
Or nous venons de voir que “AA” est égale à -Vr*sin(BETA), nous en déduisons facilement que “BB” = Vr*sin(BETA)/tg(ALPHA).
Et nous avons aussi vu que “CC” = -Vr*cos(BETA).
Et comme nous voyons sur le schéma que Vmax = BB + CC, nous avons notre formule.
Vmax = -Vr*cos(BETA) + Vr*sin(BETA)/tg(ALPHA) ce qui donne en simplifiant :
Et la vitesse du vent Apparent ?
Au point où nous en sommes, calculons la vitesse du vent apparent et nous aurons fini nos formules.Notre vent apparent c’est la grosse flèche bleue. Pythagore va nous aider avec sa formule (⋀2 signifie au carré, notation empruntée à l’informatique et beaucoup plus pratique que celle des mathématiques) :
(VentAppMax)⋀2 = (Vr*sin(BETA)/tg(ALPHA) ) ⋀2 + Vr*sin(BETA) ⋀2 et par simplification :
Ouf, la partie théorique est maintenant finie. Passons aux cas pratiques.
Quelques simulations avec les formules
Vitesse du bateau et du vent apparent
| alpha = | 40 | |
| =-COS($A5*PI()/180)+(SIN($A5*PI()/180)/TAN($B$1*PI()/180)) | =SIN(A5*PI()/180)*SQRT(1+1/(POWER(TAN(B$1*PI()/180),2))) | |
| Angle vent réel (BETA) | Vitesse Bateau Max | Vent Apparent Max |
| 30 | -0.27 | 0.78 |
| 40 | 0.00 | 1.00 |
| 50 | 0.27 | 1.19 |
| 60 | 0.53 | 1.35 |
| 70 | 0.78 | 1.46 |
| 80 | 1.00 | 1.53 |
| 90 | 1.19 | 1.56 |
| 100 | 1.35 | 1.53 |
| 110 | 1.46 | 1.46 |
| 120 | 1.53 | 1.35 |
| 130 | 1.56 | 1.19 |
| 140 | 1.53 | 1.00 |
| 150 | 1.46 | 0.78 |
| 160 | 1.35 | 0.53 |
| 170 | 1.19 | 0.27 |
| 180 | 1.00 | 0.00 |
Peut-on aller à 2 fois, 3 fois la vitesse du vent ?
| alpha = | 10 | 15 | 20 | 25 | 28 | 30 |
=-COS($A5*PI()/180)+(SIN($A5*PI()/180)/TAN(B$1*PI()/180))
| ||||||
| Angle vent réel (BETA) | Vitesse Bateau Max | Vitesse Bateau Max | Vitesse Bateau Max | Vitesse Bateau Max | Vitesse Bateau Max | Vitesse Bateau Max |
| 30 | 1.97 | 1.00 | 0.51 | 0.21 | 0.07 | 0.00 |
| 40 | 2.88 | 1.63 | 1.00 | 0.61 | 0.44 | 0.35 |
| 50 | 3.70 | 2.22 | 1.46 | 1.00 | 0.80 | 0.68 |
| 60 | 4.41 | 2.73 | 1.88 | 1.36 | 1.13 | 1.00 |
| 70 | 4.99 | 3.16 | 2.24 | 1.67 | 1.43 | 1.29 |
| 80 | 5.41 | 3.50 | 2.53 | 1.94 | 1.68 | 1.53 |
| 90 | 5.67 | 3.73 | 2.75 | 2.14 | 1.88 | 1.73 |
| 100 | 5.76 | 3.85 | 2.88 | 2.29 | 2.03 | 1.88 |
| 110 | 5.67 | 3.85 | 2.92 | 2.36 | 2.11 | 1.97 |
| 120 | 5.41 | 3.73 | 2.88 | 2.36 | 2.13 | 2.00 |
| 130 | 4.99 | 3.50 | 2.75 | 2.29 | 2.08 | 1.97 |
| 140 | 4.41 | 3.16 | 2.53 | 2.14 | 1.97 | 1.88 |
| 150 | 3.70 | 2.73 | 2.24 | 1.94 | 1.81 | 1.73 |
| 160 | 2.88 | 2.22 | 1.88 | 1.67 | 1.58 | 1.53 |
| 170 | 1.97 | 1.63 | 1.46 | 1.36 | 1.31 | 1.29 |
| 180 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
Passons maintenant à la VMG
Vous vous rappelez la VMG ? velocity made good, c’est à dire la capacité d’un bateau à aller à un point au vent (0° du vent réel) ou un point sous le vent (180° du vent réel) en schématisant un peu.
La VMG est donc simplement la projection de la vitesse du bateau sur l’axe de vent réel, ce qui correspond à la vitesse du bateau (vecteur vert) multiplié par le cosinus de l’angle (180-BETA).
Rappelons que cos(180-BETA) = - cos(BETA)
alpha =
|
30
|
40
|
Angle vent réel (BETA)
|
VMG
|
VMG
|
30
|
0.00
|
0.23
|
40
|
-0.27
|
0.00
|
50
|
-0.44
|
-0.17
|
60
|
-0.50
|
-0.27
|
70
|
-0.44
|
-0.27
|
80
|
-0.27
|
-0.17
|
90
|
0.00
|
0.00
|
100
|
0.33
|
0.23
|
110
|
0.67
|
0.50
|
120
|
1.00
|
0.77
|
130
|
1.27
|
1.00
|
140
|
1.44
|
1.17
|
150
|
1.50
|
1.27
|
160
|
1.44
|
1.27
|
170
|
1.27
|
1.17
|
180
|
1.00
|
1.00
|
Donc, pour remonter au vent, il faut être à 60° du vent réel et pour aller sous le vent à 150° du vent réel.
Hélas, ceci n’est valable que si vous êtes au près serré du point de vue du vent apparent.
- 1 radian donne 57 ° environ
- 2,6 radian donne 150° environ, ce qui corrobore bien les précédents calculs.
Mais alors, faut-il aussi que les amoureux de glisse apprennent à faire du près serré et ne plus laisser ce talent uniquement aux besogneux de croisière ;-)